Eigenfaces of UNC


In the course, 205 - Geometric & Scientific Computation, we were assigned an eigeinfaces problem for a homework. The final goal of this project was to group faces by similarity.

Shown to the right, you see that this was relatively successful. Notice that people with similar hair are grouped near each other. On the left, you can see that the two images taken under different lighting conditions are grouped together, and apart from everyone else. There are two outliers from most of the class -- distinguished mostly because of the shoulders, and long dark hair (Hi Kelly).

16 students, clustered by image similarity

8 Eigenvectors from the 201 UNC face dataset
In the top frame, you can view a very wide image which contains 201 faces from the UNC Chapel Hill computer science department.

The results were so interesting to me from the homework assignment, I decided to run the procedure again on a larger set of faces. The 201 faces were taken from the online photo directory of the department. It took me about 20 miutes to crop all the images to just the faces, and numerous hours to run the calculations. 

The data isn't as nice as the 16 faces we collected from the 205 class, however. The lighting conditions are dramatically different, as are the poses everyone was in. 

Still, I was very interested to see what the result would be from running the simulation on this very large data set. 
Above, you can see 8 of the eigenvectors from the 201 face dataset. The eigenvectors can be thought of the most prominent directions in which the images vary. The first eigenvector is the average of all the faces. For this dataset, the properties captured by the eigenvectors can be described. The second eigenvector captures the overall brightness of the face in the picture. The third and forth capture direction from which the face was illuminated. The fourth captures a bit of face shape. 

The rest of the eigenvectors (there are 201 of them) continue to capture more subtle details. The eigenvectors are ordered by the amount that the data is distributed by their direction. 

The eigenvectors are obtained by a Singular Value Decomposition (SVD). From these, a set of vectors can be created which provide a basis for the dataset. Each image is a vector in 15,400 dimensions (140 x 110 pixels). The basis, created by taking the difference of each eigenvector (2 thru 201) with the first eigenvector, is of only 200 dimensions. 

A distance can be calculated between each of the 201 images in this 200 dimensional basis. Then, a spring mass system can be constructed, such that a spring between each face has a rest length equal to the distance between the faces. 

The spring mass system can be forced into only two dimensions, so that we may look at it easily. To do this, each face is given a random starting position, and then the spring mass system allowed to bounce around until it comes to a relaxed and stable state.

To the right you can see a plot of the spring mass system positions as they converge to a stable system. 

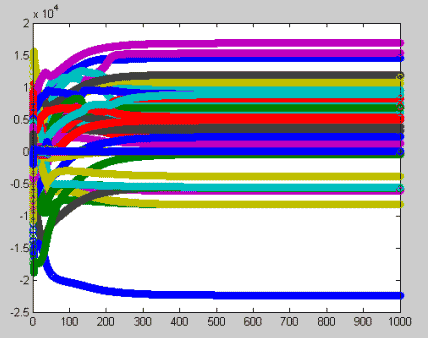
The convergence of the spring mass system for 16 images

 

Analysis of the 201 face dataset

The 201 faces did not cluster as nicely as the 16 faces did. 

It is clear that the 201 faces arranged themselves very well with respect to their overall brightness. This is easy to understand, as the second eigenvector captured this property, and it's magnitude was 5 times as great as the next eigenvector. 

Looking through the faces, you will see they cluster occasionally by hair mass, lighting, or bright foreheads. The easiest to see is the hair mass. People was a good area of dark hair on top group together. 

These lesser properties create only some small groups however -- and the small groups are held far apart by the dominating lighting conditions. 

It's still pretty nifty to see all 201 images arranged. =) And if you know some of us, well, wave and say "hi". Can you find me? I'm the only face in profile.