Summary:

Implement a small program to simulate particle dynamics (a cannon shooting and a mass on a spring). Use several numerical integration methods.

Assignment text:
 

Due on Wednesday, Feb 13, 2002  (10pt) Problem A: Ballistic Motion Given a location of a gun at (0,0,0), write an 3D artillery simulator that can take in the mass of the projectile, amount of powder, the azimuth and elevation of the gun barrel. Use the amount of powder and the mass of the projectile to determine the muzzle velocity. Account for gravity and air friction. Assume that one kilogram of powder produces 10,000 newtons of force. Assume instantaneous acceleration as a result of the powder going off. Air friction coefficient is constant. Set it to be 50 kg/s initially. The gun and target are both on the X-Z plane.  (15pt) Problem B: Spring-Mass Simulator A spring hands vertically in its equilibrium or resting position. Given a user-defined mass m attached to the spring with the spring constant k, not stretched at first. Simulate the motion of the spring and mass under the effects of spring and gravitational forces. Assume the mass is 5 kg and k = 15 kg/s^2. Then, set the mass to be 10 kg and k = 20 kg/s^2.  For both problems, you'll need to write at least two functions (Euler's method vs. Mid-point or 4th order Runge-Kutta) for integration and compare their numerical accuracy and stability. Which function is more accurate? Which one is more stable? Which one is more efficient?  This assignment will be graded based upon:  Correctness of the implementations (50%)  UI & other SE factors (30%)  Other features (analysis, etc.) (20%)

What I did:

I have created a small program.
download the program (you need to put qt-mt230nc.dll in the same directory)

It requires Windows (2000?), openGL, GLVU (to compile), and the QT runtime dll (included).

You can view the source code. All the simulation code is contained in the main.cpp. The other files are used for the user interface.
 

I have implemented the following integration methods:

• Euler
• x(t+dt) = x(t) + v(t)*dt
• v(t+dt) = v(t) + a(t)*dt
• Midpoint
• x_k1 = v(t)*dt
• v_k1 = a(t)*dt
•  
• x_k2 = (x(t)+.5*x_k1)*dt
• v_k2 = (v(t)+.5*v_k1)*dt
•  
• x(t+dt) = x(t) + x_k2
• v(t+dt) = v(t) + v_k2
• Runga-Kutta Fourth Order (RK4)
• x_k1 = v(t)*dt
• v_k1 = a(t)*dt
•  
• x_k2 = (x(t)+.5*x_k1)*dt
• v_k2 = (v(t)+.5*v_k1)*dt
•  
• x_k3 = (x(t)+.5*x_k2)*dt
• v_k3 = (v(t)+.5*v_k2)*dt
•  
• x_k4 = (x(t)+x_k3)*dt
• v_k4 = (v(t)+v_k3)*dt
•  
• x(t+dt) = x(t) + x_k1*1/6 + x_k2*1/3 + x_k3*1/3 + x_k4*1/6
• v(t+dt) = v(t) + v_k1*1/6 + v_k2*1/3 + v_k3*1/3 + v_k4*1/6
• Implicit (backwards Euler)
• For cannon balls:
• v(t+dt) = (v(t)+dt*gravity)/(1+dt*WindResistance/BallMass)
• x(t+dt) = x + dt*v(t+dt)
• For spring mass:
• v(t+dt) = (v(t)-dt*SpringConstant/Mass*x(t)+dt*gravity) / (1+dt*dt*SpringConstant/SpringMassMass)
• x(t+dt) = x + dt*v(t+dt)

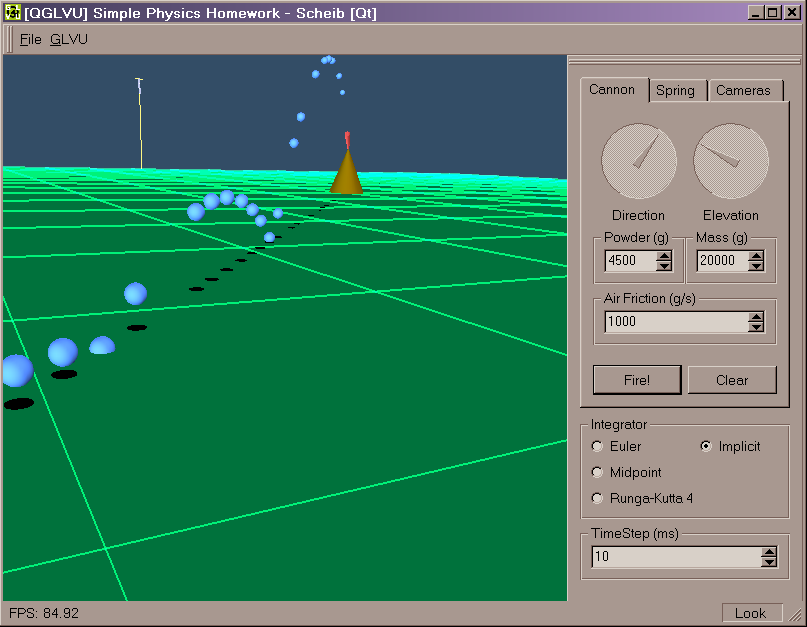
I found that all integration methods worked similarly for small time steps (10ms). The hanging spring performed poorly for large time steps (50ms, 100ms) with Euler and Midpoint. The mass on the spring would gain energy and "explode". RK4 performed well, but still gained energy.

The implicit solver removes energy from the system slowly, however it is far more stable. Shots from the cannon do not go as far, and the spring mass dampens out and will eventually stop moving. These effects are slight, but become more apparent at very large time steps (100ms or more).